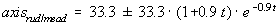
Calculations
When we take a closer look, the diagram in figure 3 appears to contain far more information than we would think on the face of it. We will now focus entirely on figure 3. which will be examined from a mathematical point of view. The figure clarifies two developments: the recovery of the soil and, superposed on that, the wavy pattern occurring during the recovery. The two patterns will be dealt with independently of each other.
Plant species demonstrate a wavy pattern so it is natural to consider the recovery of the soil after working with the rotary cultivator in terms of a wavy phenomenon. It is a vibration that is so subdued that no deflection can be seen. It is a disturbance returning to its rest in a flowing movement: a critically subdued oscillator.
The curved axes in figure 3 comply with the following formula:
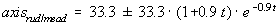
The half-life is about 1 year
The wavy phenomenon is unrelated to this. The three waves appear to have their own wavelengths:
Tr = 3 years, Tw = 4 years, Tm = 3.5 years
while at the same time rud + wood + mead = 100
There are three waves the sum of which equals 100. This reminds us of the Fourier analysis of a straight line. Nature seems to apply this in practice.
There is another connection between the three waves which can scarcely be deduced from figure 3 because it is plotted in percentages. The connection is found when taking logarithms of the measuring points thereby first eliminating the disturbance of the soil. From figure 5 the following appears:
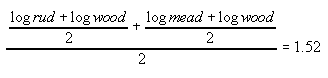
This is the energy equation. In case a wave appears, this formula will indicate how the energy supplied will be divided among the three groups of wood, ruderal and meadow. If the waves are roughly of the same large amplitude, the wood will be apportioned most of the energy. If we let nature go its own way, a wood is certain to develop with a few ruderal and meadow spots. This is indicated with arrows in figure 4 .
In figure 5 , the logarithms of the measuring points are drawn based on the fact that the points in figure 3 only slightly deviate from the corresponding axis.
According to the following formula: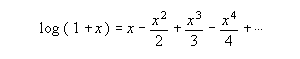
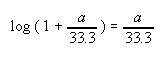 while
while
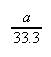 has a maximum value of
has a maximum value of
![]()
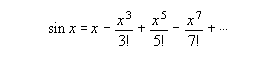
It is now possible to leave the logarithmic formula for what it is and move on to the sine formula as a result of which the measuring points in figure 3 can be soundly connected to each other through sine curves.
Still, the lines drawn in figure 3 cannot refer to pure sines. There is an interaction between the three groups of plants.
A meadow plant or ruderal plant cannot grow on the spot of a wood plant and vice versa. The meadow is furnished with a carpet of plants by mutual "arrangement". An energy-supplying wave has a favourable effect on one group but works out badly for the other two. Each of the three waving curves in figure 3 has resulted out of the cooperation between two waves originating from the two other groups.
The goniometrical formula :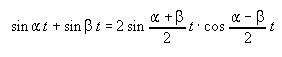
expresses how two initially independent waves will act after they enter into a cooperation. A linking is brought about, the sine in the second term, but a beat is developing as well, the cos. After calculation of the primary waves the energy source is found that causes the waving curves in figure 3 .
We will refer to the primary waves as Rud, Wood and Meadow, sometimes R, W, and M.
An undamped, time-dependant (t) sine can be referred to as follows:
![]()
The factor ![]() can be calculated on the basis of the following equations:
can be calculated on the basis of the following equations:
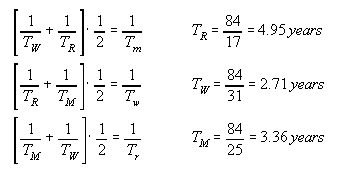
Using the primary waves R, W and M the waves found in figure 3 can be constructed ( figure 6 ). To this end, the amplitude of the wood should be slightly smaller than those of the two other waves (2.8% and 3.9%). Consequently, the beats will not be extinguished altogether. Some movement will remain. As a result, the chemical reactions in nature cannot come to a standstill.
The reacting components will be kept in a constant motion.
Combined with the oscillator, we now have a total picture of
figure 3
and
figure 7
.
The primary waves R,W and M are found in the sun wind.
| Rozelot (5) mentions the following periods : | 4.90 years | 3.75 years | 2.83 years | |
| while our calculations resulted in : | 4.95 years | 3.36 years | 2.71 years |
The sun wind, however, does not reach the earth. Geomagnetism bends it off to the poles thus creating northern lights and southern lights. However, there is also the damaging cosmic radiation which is partly blown away but the part that hits the earth will have been modulated by the sun wind. This part of the cosmic radiation can carry the modulation to the earth as a result of which subterranean life is disturbed, each species to a different degree. In the process, the sun wind is reflected twice in relation to the axis. In turn, the influence on the soil is in phase with the sun wind. This is manifest in the plant groups ruderal, wood and meadow. The influence is observed by us as a decelerated one because we have to wait for the seed to germinate and grow into plants that we can identify. This delay takes at least six months. On the basis of this we can conclude that the sun wind has a favourable influence on the plants. Looking back, the result is less surprising than it first seemed. In tree rings (see Cambridge (4)) , the influence of the sun wind was found to be evident. It is therefore not surprising if the influence in some form can also be observed in herbs. After all, plants originated when cosmic radiation and sun wind already existed. They will be adapted to anything that regularly occurs in nature.
figure 8 gives a more general summary of the aforementioned. The revolution of the earth too must be tuned to the sun wind, something which will have taken place at the origin of the planetary system. One can imagine this in the presence of a strong magnetic field.
| next |